Playing Evolution with Intransitive Dice
3 January 2023, Julius B. KirkegaardWe are going to be playing some games of chance and try to gain insight into the evolution of species that interact intransitively.

We are going to be playing some games of chance and try to gain insight into the evolution of species that interact intransitively.
Everyone is familiar with games of chance. From pure luck games such as the slot machine in casinos to games that involve mostly skill like football matches (indeed worse teams sometimes win over better ones).
The most well-known game of chance is perhaps the rolling of dice. Here's a die you can try throwing:
Here are two standard dice (with sides 1-2-3-4-5-6). Let's call them A and B. If we roll them both, we can see who wins the `fight´.
Obviously, they are equally likely to win.
The outcome of a single roll of two dice is very random. If we repeatedly roll the dice and count who wins, we can judge who wins in the long run.
In this case, as the two dice are precisely the same, they perform very similarly and typically end up with almost the same number of wins.
Now let's have die B evolve into a better die. One might call this cheating, but rarely do people refer to a lion having cheated in the game of evolution.
Now the new B' has sides 3-4-5-5-6-8, which is much better than the standard die.
Let's try the repeated competition with this set of dice:
Clearly die B' is the better one.
It is pretty clear why die B' is much better than die A. Most obviously, its sides sum to a much bigger number (31) than the standard die (21).
1 2 3
4 5 6
3 4 5
5 6 8
Now consider these dice:
3 3 3
3 3 6
2 2 2
5 5 5
1 4 4
4 4 4
All of their sides sum to the same number (21). However, this does not mean that they are equally good! Do you have any preference?
Let us experiment and see who is better:
So clearly, die α is better than die β. And die β is better than die γ. We can write this as α ≻ β and β ≻ γ.
This does seem like it is implying that α is the best die of the three.
However, there is one competition we still need to run:
The result is γ ≻ α, and we are left to conclude
α ≻ β ≻ γ ≻ α
which seems very unnatural compared to e.g. integers:
3 > 2 > 1 > 3 (obviously wrong)
What we just discovered is that dice can behave intransitively. Another way to say this is that the relationship between dice can be circular.
This is similar to the game of rock-paper-scissors
🪨 ≺ 📜 ≺ ✂ ≺ 🪨
but with an element of chance as well.
Surprisingly, such intransitive interactions are found in biological systems ecosystems as well, and might be important for understanding biodiversity.
We are going to be playing evolutionary games with dice. Instead of a genome consisting of the four letters of DNA, we take the numbers on the sides of the dice as our genome. Mutations in the dice genes will directly affect a die's competitive behavior ("its phenotype").
Let us set some rules for how dice can evolve. Three will suffice:
Mutations change just one number, one step (+ 1 or - 1).
The smallest possible number on a die is 1.
The sum of the sides of a die may never exceed 21.
Let us try it:
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
1 2 3
4 5 6
Mutations are random and we do not necessarily obtain better dice by doing mutations. In fact, as we in this example began at the fitness ceiling, we are quite likely to end up with a worse die than we started with.
Now let us consider two populations of dice. In both populations, all dice have the same sides. Instead of the standard die, we go with:
1 1 1
6 6 6
1 1 1
6 6 6
The rules are simple: dice compete 1v1, and the loser gets replaced by a copy of the winner.
If you repeatedly run this experiment, you should find that the outcome is random: which population ends up the largest changes from run to run. This is natural, as the two populations start out exactly the same. However, if we ran this experiment long enough, one of the populations would die out from stochastic extinction. This is an example of the competitive exclusion principle.
Now let us consider again two populations of dice, starting with sides 1-1-1-6-6-6, but where one is static and the sides of these dice never change, and another is evolving, such that after every round each die has a chance to evolve according to the mutation rules.
What you should observe is that the static population wins initially. This is because the mutations are very likely to move the dice away from the global fitness ceiling, and thus, on average, the mutations make the dice worse.
However, the evolving population has the long-term advantage that it can find a set of mutations that out-competes the static die 1-1-1-6-6-6. Thus, the evolving population wins in the long run.
So we have just seen that evolution is a good thing. Can there be such a thing as too much? Let us try to have two populations that both evolve, but one faster than the other:
This competition goes a bit back and forth, but in the end we see that the slow-evolving population out-competes the fast one. Thus, we have found that random mutations are good for a population, but too many of them are bad.
On evolutionary timescales, nature does not divide its population of species into distinct groups. All species on Earth have evolved from a common ancestor by speciation.
Starting with a population of dice, we can study speciation by defining two dice to be different species when their "genome" (the numbers on their sides) differ by some amount. If we use many-sided dice (i.e. more than 6), we can obtain quite complex ecosystems of dice from mutations and competition alone.
It is common to think of evolution as optimization. But in our system of dice, there is no global measure of optimality. How good a die is depends on the remaining dice of the system. We have thus developed an exceedingly simple model for co-evolution.
We have glossed over one critical aspect though: the outcome of our model depends on the mutation rate of the species. This is a species feature that should also be adaptable but on much slower time scales than that of mutations themselves.

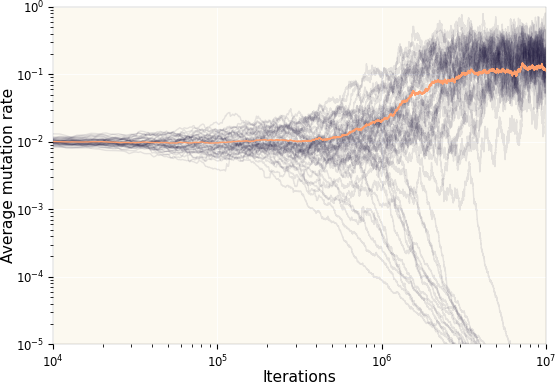
If we allow the mutation rate itself to mutate, a critical question to ask is whether this will be driven to zero or not? In other words, can our system maintain the stability of many species?
The plot explores exactly this by considering 2500 dice that start out with a small mutation rate (=0.01). As can be observed, the mutation rate reaches a meta-stable state with a large mutation rate. This is a practical illustration of the Red Queen hypothesis which argues that species may never stop evolving in order to avoid extinction.
(unfortunately, this example is way too slow to run the simulation in the browser)Co-evolution is a complex subject, but playing with dice can illuminate many of the complexities in a very simple framework.